Moment Of Inertia Formula For Rectangular Beam slideshare
Master i-section on CalcTree. Free-to-Use i section moment of inertia calculator for structural analysis. Calculate now!
Moment Of Inertia Beam Torsional Moment Of Inertia Rectangular Beam
Fundamentally, the moment of inertia is the second moment of area, which can be expressed as the following: Ix = ∫ ∫y2dA I x = ∫ ∫ y 2 d A Iy = ∫ ∫x2dA I y = ∫ ∫ x 2 d A To observe the derivation of the formulas below, we try to find the moment of inertia of an object such as a rectangle about its major axis using just the formula above.
Moment of Inertia Examples YouTube
This tool calculates the moment of inertia I (second moment of area) of an I/H section (also called W-beam or double-T). The flanges are assumed equal. Enter the shape dimensions h, b, t f and t w below. The calculated results will have the same units as your input. Please use consistent units for any input. Looking for another axis? ADVERTISEMENT

Moment Of Inertia Formulas For Different Shapes Structural Basics
Area moment of inertia, also known as second area moment or 2 nd moment of area, is a property of a two-dimensional plane shape, where it shows how its points are dispersed in an arbitrary axis in the cross-sectional plane. This property basically characterises the deflection of the plane shape under some load.
I Beam Moment Of Inertia Equation sharedoc
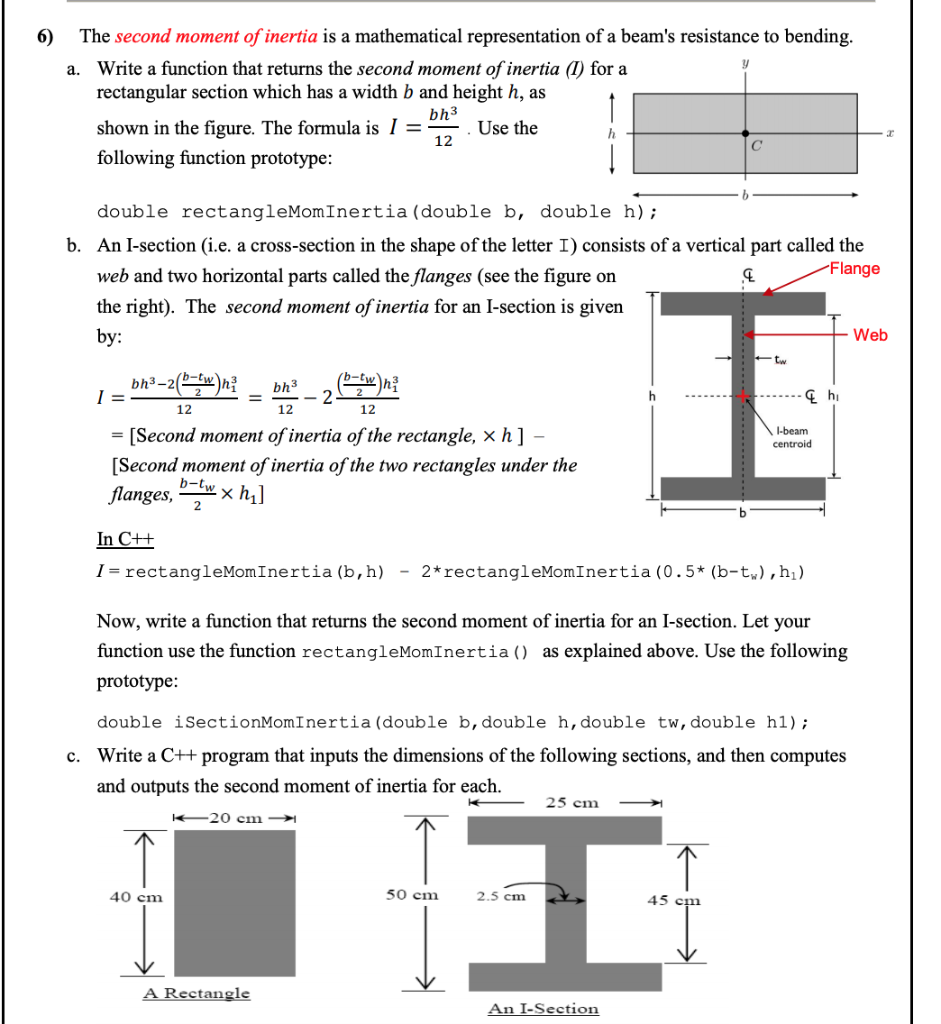
Moment of Inertia (Iz, Iy) - also known as second moment of area, is a calculation used to determine the strength of a member and it's resistance against deflection. The higher this number, the stronger the section. There are two axis here:

Area Moment of Inertia Sistemas estruturais, Engenharia e construção
The moment of inertia (second moment or area) is used in beam theory to describe the rigidity of a beam against flexure. The bending moment M applied to a cross-section is related with its moment of inertia with the following equation: where E is the Young's modulus, a property of the material, and.

Area Moment of Inertia in Beams YouTube
Notice that the centroidal moment of inertia of the rectangle is smaller than the corresponding moment of inertia about the baseline. The solution for \(\bar{I}_{y'}\) is similar. Thinking Deeper 10.2.4. Stresses in a Rectangular Beam. To provide some context for area moments of inertia, let's examine the internal forces in a elastic beam.

Moment Of Inertia For Standard I Beam New Images Beam
RESULTS DATA I x - Area moment of inertia about centroidal axis X; I y - Area moment of inertia about centroidal axis Y; A - Section area; σ - Bending stress in cross section (on side B). Metric Imperial Height (H) Width (B) Shelf thickness (t) Wall thickness (s) Moment of inertia (I x) Moment of inertia (I y) Section area (A) Bending moment (M x)
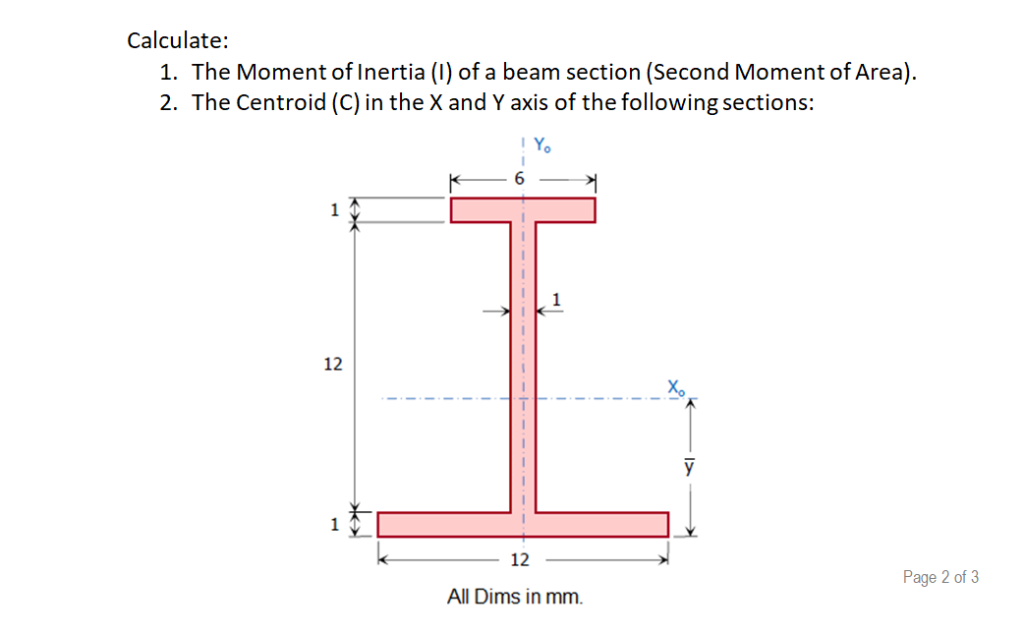
Solved Calculate 1. The Moment of Inertia (I) of a beam
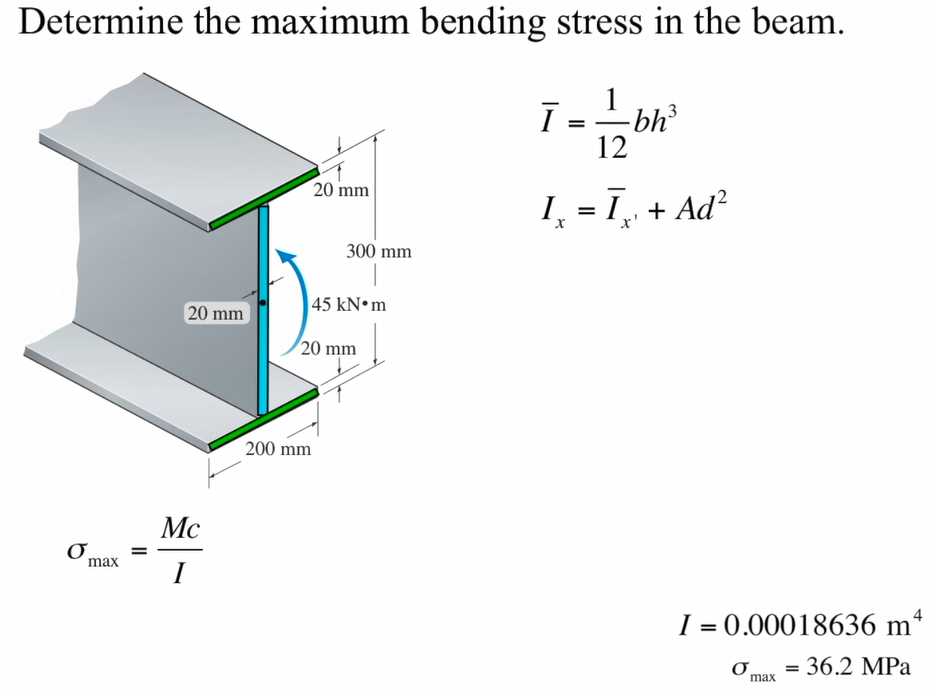
The area moment of inertia, also called the second moment of area, is a parameter that defines how much resistance a shape (like the cross-section of a beam), has to bending because of its geometry. Consider a thin plank that supports a 100 kg load. The plank will be much less stiff when the load is placed on the longer edge of the cross-section.
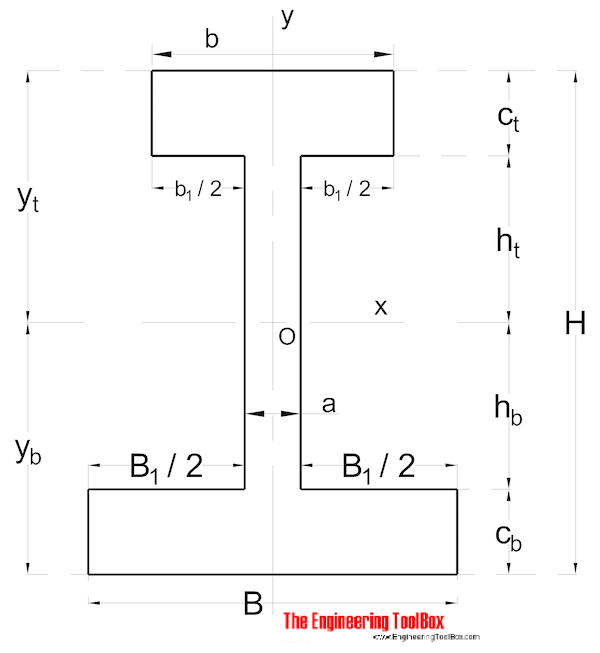
Area Moment of Inertia Typical Cross Sections I
The area moment of inertia, also known as the second moment of area, is a property of a shape that measures its resistance to bending or deformation. It plays a significant role in structural engineering, especially in analyzing beams subjected to bending moments.
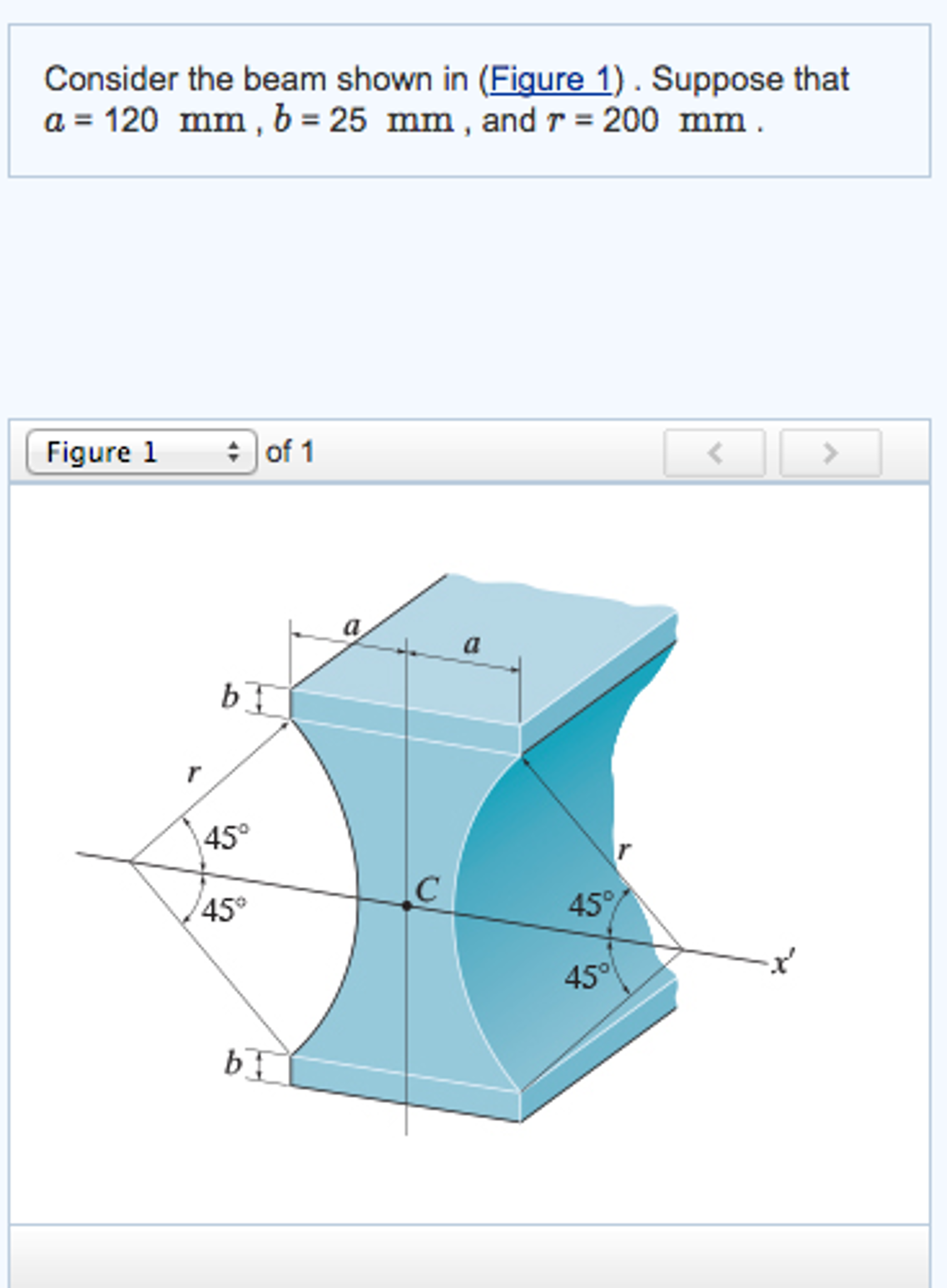
Moment Of Inertia For Beam All in one Photos
Second Moment of Area is defined as the capacity of a cross-section to resist bending. Note: Use dot "." as decimal separator. Second Moment of Area Formula: Supplements: Standard Beam Channel Sizes Dimensions Section Properties Calculators Reference: Oberg, E. , Jones ,F.D. , Horton H.L. , Ryffel H.H., (2016) . Machinery's Handbook . 30th edition.

I Beam Moment Of Inertia Equation New Images Beam
z max ( x = 0) =. F · l03. 3 Y · IA. F is the applied point force at the end of the beam, l0 is the length of the beam, Y is Young's modulus of the (homogeneous) material in use, and IA is the area moment of inertia containing all information about the cross-sectional geometry of the beam relative of the direction of bending. zmax is the.
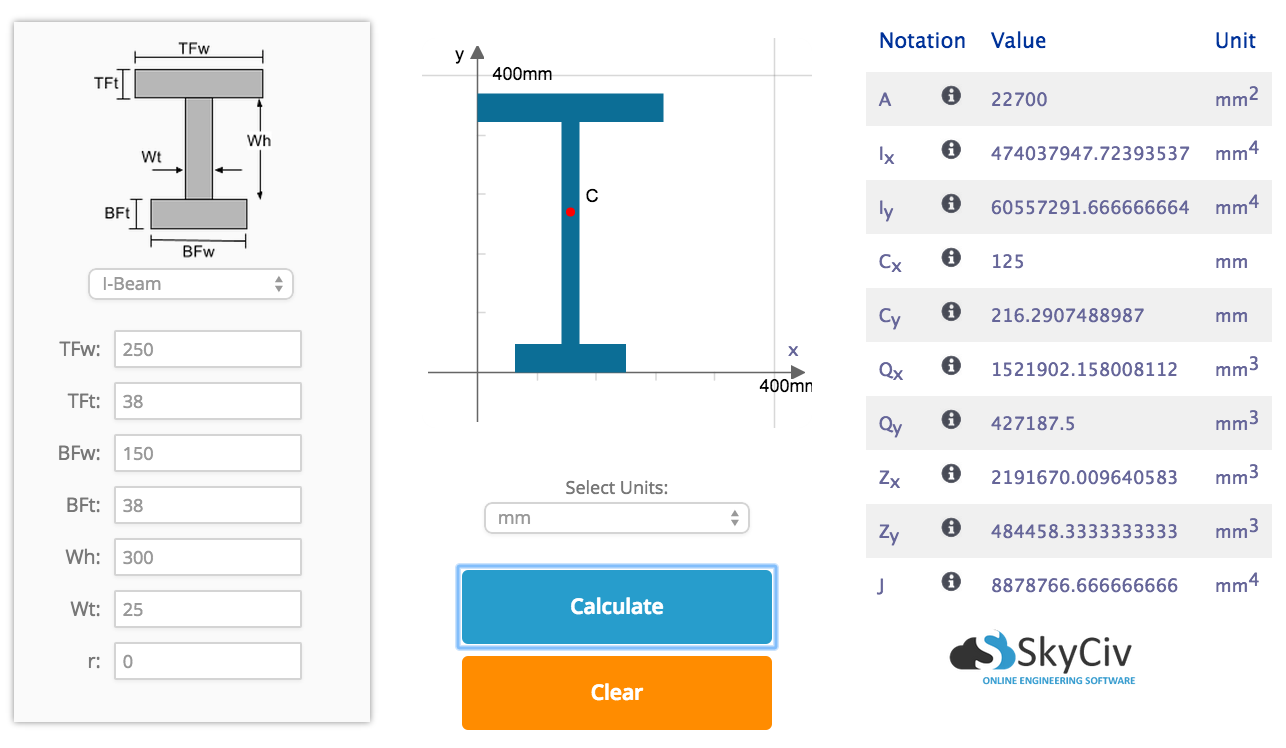
Moment of Inertia of Beam Sections SkyCiv
Area Moment of Inertia, Moment of Inertia for an Area or Second Moment of Area for typical cross section profiles. Area Moment of Inertia Converter Convert between Area Moment of Inertia units. Beams - Fixed at Both Ends - Continuous and Point Loads Stress, deflections and supporting loads.

Moment of Inertia of an I Section YouTube
The moment of inertia is a crucial parameter in calculating the bending stresses to verify structural objects such as beams, columns and slabs. By understanding the calculation of the moment of inertia, you are one step closer to designing an I- or H-Beam. 🔥🔥
How To Calculate Plastic Section Modulus Of An I Beam Home Interior
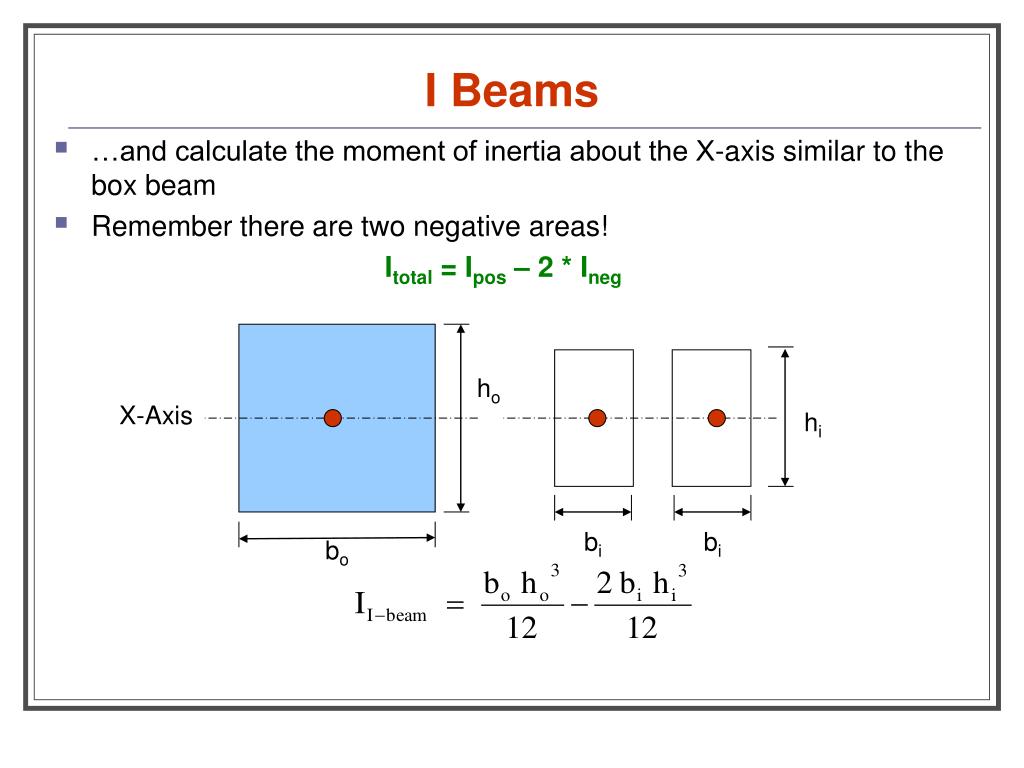
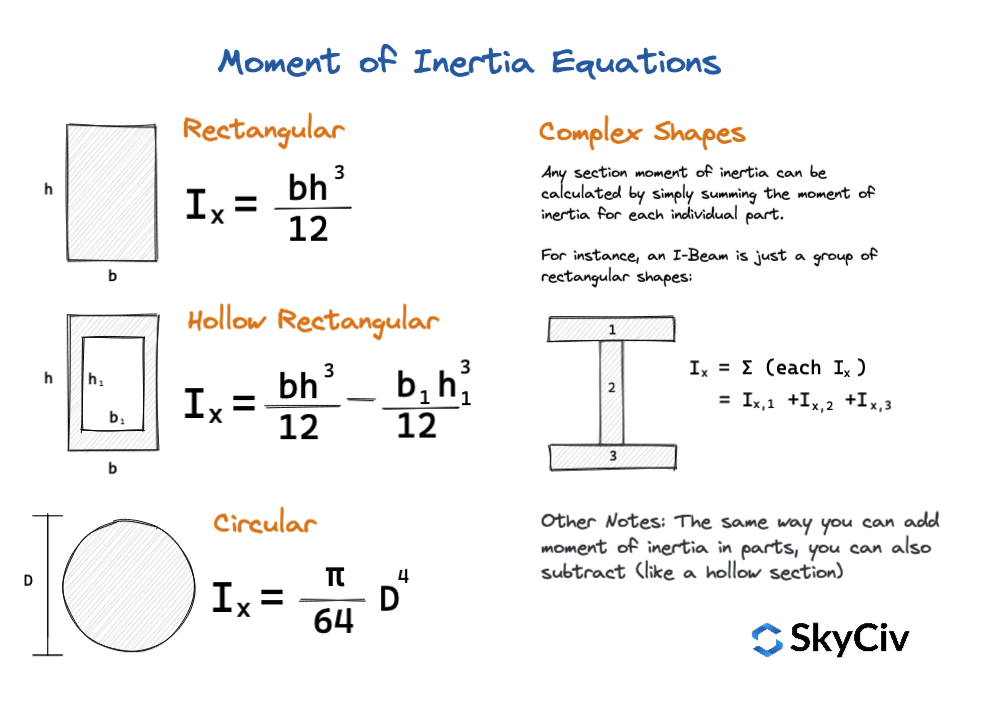
Step 1: Segment the beam section into parts When calculating the area moment of inertia, we must calculate the moment of inertia of smaller segments. Try to break them into simple rectangular sections. For instance, consider the I-beam section below, which was also featured in our centroid tutorial.

Moment Of Inertia Beam Torsional Moment Of Inertia Rectangular Beam
The moment of inertia, or more accurately, the second moment of area, is defined as the integral over the area of a 2D shape, of the squared distance from an axis: where A is the area of the shape and y the distance of any point inside area A from a given axis of rotation.